Introduction to multi-edge network inference in R using the ghypernet-package
European Symposium on Societal Challenges in Computational Social Science - 2019 - EuroCSS
September 2, 2019: Half-day workshop, Morning session
The half-day workshop provides an introductory tutorial on Network Regression Models (NRMs) for multi-edge networks. Network models are the most important tools in network science for the analysis of complex systems.
Currently, the estimation of models for large systems is hampered by the computational burden posed by numerical simulations on which most models rely. For this reason, analytical models and models that do not rely on simulations for the estimation of their parameters are the optimal approach to deal with large-scale complex systems.
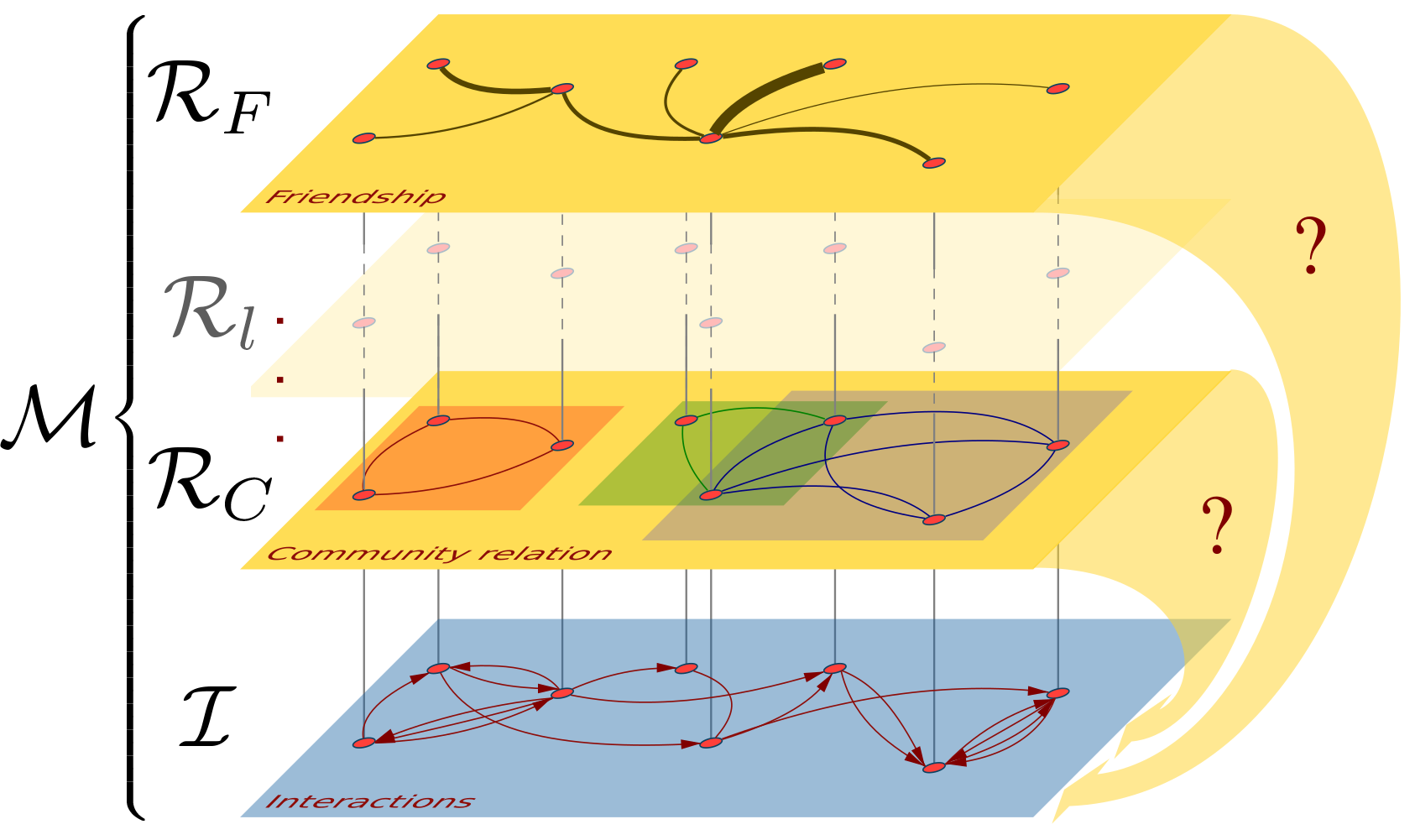
In this workshop, we present a new network inference model based on generalised hypergeometric ensembles. These are a recently developed class of analytically tractable ensembles for multi-edge networks. They contain random graphs generated by fixing degree sequences, and incorporating arbitrary propensities of nodes pairs to be connected. NRMs allow to estimate the effect size and significance as predictors in a regression of known relations between nodes. This is achieved by incorporating such relations in the ensemble, in an attempt to model the original data. As the model does not rely on numerical simulations, it is easy to apply, fast and well-suited for large-scale networks.
Register for the workshop here.
Prerequisites: All analyses are performed in R using the R-package 'ghypernet'. Participants should be familiar with base-R commands as well as basic network concepts.
Event format: The workshop is split into three parts: After an introduction to hypergeometric ensembles, we demonstrate some empirical applications. We then provide an extensive lab session where participants are will get a chance to test the model hands-on (either with their own data or some example data provided by us).
References
Quantifying Triadic Closure in Multi-Edge Social Networks
|
[2019]
|
|
Brandenberger, Laurence;
Casiraghi, Giona;
Nanumyan, Vahan;
Schweitzer, Frank
|
ASONAM '19: Proceedings of the 2019 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining
|
more» «less
|
Abstract
Multi-edge networks capture repeated interactions between individuals. In social networks, such edges often form closed triangles, or triads. Standard approaches to measure this triadic closure, however, fail for multi-edge networks, because they do not consider that triads can be formed by edges of different multiplicity. We propose a novel measure of triadic closure for multi-edge networks of social interactions based on a shared partner statistic. We demonstrate that our operalization is able to detect meaningful closure in synthetic and empirical multi-edge networks, where common approaches fail. This is a cornerstone in driving inferential network analyses from the analysis of binary networks towards the analyses of multi-edge and weighted networks, which offer a more realistic representation of social interactions and relations.
Generalised hypergeometric ensembles of random graphs: The configuration model as an urn problem
|
[2018]
|
|
Casiraghi, Giona;
Nanumyan, Vahan
|
arXiv:1810.06495
|
more» «less
|
Abstract
We introduce a broad class of random graph models: the generalised hypergeometric ensemble (GHypEG). This class enables to solve some long-standing problems in random graph theory. First, GHypEG provides an elegant and compact formulation of the well-known configuration model in terms of an urn problem. Second, GHypEG allows incorporating arbitrary tendencies to connect different vertex pairs. Third, we present the closed-form expressions of the associated probability distribution ensures the analytical tractability of our formulation. This is in stark contrast with the previous state-of-the-art, which is to implement the configuration model by means of computationally expensive procedures.
Multiplex Network Regression: How do relations drive interactions?
|
[2017]
|
|
Casiraghi, Giona
|
arXiv e-print
pages: 1-17
|
more» «less
|
Abstract
We introduce a statistical method to investigate the impact of dyadic relations on complex networks generated from repeated interactions. It is based on generalised hypergeometric ensembles, a class of statistical network ensembles developed recently. We represent different types of known relations between system elements by weighted graphs, separated in the different layers of a multiplex network. With our method we can regress the influence of each relational layer, the independent variables, on the interaction counts, the dependent variables. Moreover, we can test the statistical significance of the relations as explanatory variables for the observed interactions. To demonstrate the power of our approach and its broad applicability, we will present examples based on synthetic and empirical data.
Generalized Hypergeometric Ensembles: Statistical Hypothesis Testing in Complex Networks
|
[2016]
|
|
Casiraghi, Giona;
Nanumyan, Vahan;
Scholtes, Ingo;
Schweitzer, Frank
|
ArXiv e-prints
|
more» «less
|
Abstract
Statistical ensembles define probability spaces of all networks consistent with given aggregate statistics and have become instrumental in the analysis of relational data on networked systems. Their numerical and analytical study provides the foundation for the inference of topological patterns, the definition of network-analytic measures, as well as for model selection and statistical hypothesis testing. Contributing to the foundation of these important data science techniques, in this article we introduce generalized hypergeometric ensembles, a framework of analytically tractable statistical ensembles of finite, directed and weighted networks. This framework can be interpreted as a generalization of the classical configuration model, which is commonly used to randomly generate networks with a given degree sequence or distribution. Our generalization rests on the introduction of dyadic link propensities, which capture the degree-corrected tendencies of pairs of nodes to form edges between each other. Studying empirical and synthetic data, we show that our approach provides broad perspectives for community detection, model selection and statistical hypothesis testing.
|
